En ingenieria electrica un sistema polifásico es un sistema de producción, distribución y consumo de energia electrica formado por dos o más tensiones iguales con diferencia de fase constante, que suministran energía a las cargas conectadas a las líneas. En un sistema bifásico la diferencia de fase entre las tensiones es de 90°, mientras que en los trifásicos dicha diferencia o desfase es de 120°. Los sistemas trifacicos son los utilizados en la generación, transmisión y distribución de la energía eléctrica. Históricamente han existido sistemas de mayor número de fases, v.g., hexafásicos y dodecafásicos, destinado a alimentar rectificadores de modo de obtener una tensión continua poco ondulada.
Sistemas monofasicos
Es aquel que consta de una unica corriente alterna o fase y por lo tanto todo el voltaje varia de la misma forma.El voltaje y la frecuencia de esta corriente depende del pais o de la region siendo 230 y 115 voltios los valores mas extendidos para el voltaje y 50 o 60 hercios para la frecuencia.
Sistemas trifasicos
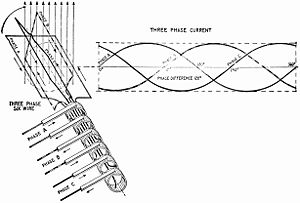
Un sistema trifásico es un sistema de producción, distribución y consumo de energia electrica formado por tres corrientes alternas monofásicas de igual frecuencia y amplitud que presentan una cierta diferencia de fase entre ellas, en torno a 120°, y están dadas en un orden determinado. Cada una de las corrientes monofásicas que forman el sistema se designa con el nombre de fase.
Un sistema trifásico de tensiones se dice que es equilibrado cuando sus corrientes son iguales y están desfasados simétricamente.
Cuando alguna de las condiciones anteriores no se cumple, el sistema de tensiones es un desequilibrado o más comúnmente llamado un sistema desbalanceado.
Recibe el nombre de sistema de cargas desequilibradas el conjunto de impedancias distintas que dan lugar a que por el receptor circulen corrientes de amplitudes diferentes o con diferencias de fase entre ellas distintas a 120°, aunque las tensiones del sistema o de la línea sean equilibradas o balanceadas.
El sistema trifásico presenta una serie de ventajas como son la economía de sus líneas de transporte de energía y de los transformadores utilizados, así como su elevado rendimiento de los receptores, especialmente motores, a los que la línea trifásica alimenta con potencia constante y no pulsada, como en el caso de la línea monofásica.
Los generadores utilizados en centrales eléctricas son trifásicos, dado que la conexión a la red eléctrica debe ser trifásica (salvo para centrales de poca potencia). La trifásica se usa mucho en industrias, donde las máquinas funcionan con motores para esta tensión.
Existen dos tipos de conexión; en triángulo y en estrella. En estrella, el neutro es el punto de unión de las fases.
Transferencia constante de potencia con cargas balanceadas
Consideremos un sistema trifásico de tensiones
Asumimos la carga balanceada. Así, en cada fase hay impedancia
con corriente de pico
y corrientes instantáneas
Las potencias instantáneas en las fases son
Usando identidades trigonometricas:
que se suman para producir la potencia instantánea total
Como los términos en corchetes constituyen un sistema trifásico simétrico, ellos suman zero y la potencia total resulta constante
o, sustituyendo la corriente de pico,

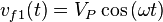





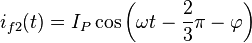
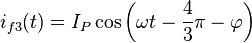



![p_{f1}(t)=\frac{V_P I_P}{2}\left[\cos\varphi+\cos\left(2\omega t-\varphi\right)\right]](http://upload.wikimedia.org/math/d/6/a/d6acbc379041613290a4940421efbe5a.png)
![p_{f2}(t)=\frac{V_P I_P}{2}\left[\cos\varphi+\cos\left(2\omega t-\frac{4}{3}\pi-\varphi\right)\right]](http://upload.wikimedia.org/math/c/6/0/c60d5cc8429a279eb79b83d061f466b6.png)
![p_{f3}(t)=\frac{V_P I_P}{2}\left[\cos\varphi+\cos\left(2\omega t-\frac{8}{3}\pi-\varphi\right)\right]](http://upload.wikimedia.org/math/b/5/6/b566257093f9450391b5f810267dd56f.png)
![p_{TOT}(t)=\frac{V_P I_P}{2}\left\{3\cos\varphi+\left[\cos\left(2\omega t-\varphi\right)+\cos\left(2\omega t-\frac{4}{3}\pi-\varphi\right)+\cos\left(2\omega t-\frac{8}{3}\pi-\varphi\right)\right]\right\}](http://upload.wikimedia.org/math/8/4/5/84592ab55af333ef6268b2f25534787d.png)

